Hien M. Nguyen and Gary H. Glover
Volume: 60, Issue: 10, Page(s): 2867 – 2877
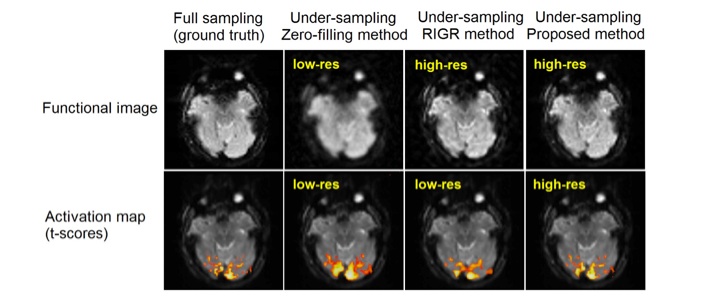
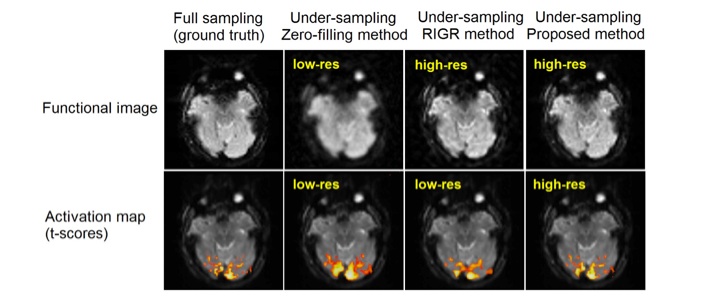
In functional MRI, it is often desirable to reduce the readout duration to make the acquired data less prone to T2* susceptibility artifacts. In addition, a shorter readout length allows for a shorter minimum TE, which is important for optimizing SNR. This can be achieved by under-sampling the k-space. However, the conventional Fourier transform-based reconstruction method suffers from under-sampling artifacts such as high-frequency ringing and loss of resolution. To address this problem, we revisit the constrained-model approach using generalized-series (GS) which has been proposed to address the under-sampling problem for dynamic MRI. We propose a modification to the conventional use of the model in order to reflect small hemodynamic signal changes typical in fMRI. Specifically, while realizing that having high model order is necessary to capture missing information, we found that it is not necessary to span all frequencies of GS basis functions uniformly. Instead, having k-space and GS “sampling” trajectories covering low-frequencies uniformly while spanning high frequencies sparsely, was observed to be an efficient strategy. The ability of the method over the conventional GS approach in improving resolution of functional images and activation maps while reducing under-sampling ringing is demonstrated by simulations and experiments at 3T. Reduction in the readout time allowed an increase of statistical signal power as compared to the fully-sampled acquisition. Unlike compressed sensing approaches, the proposed method is linear and hence has lower computational complexity. This method can also be applicable to other temporal imaging modalities where the temporal signal change of interest is typically much smaller than the baseline component.