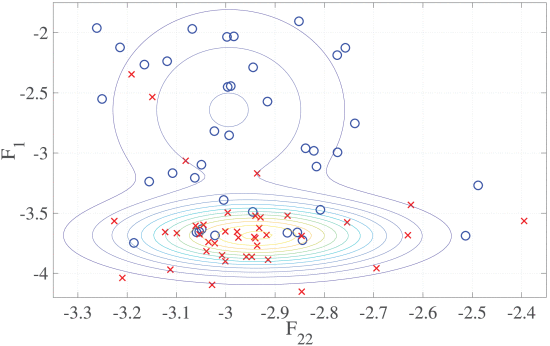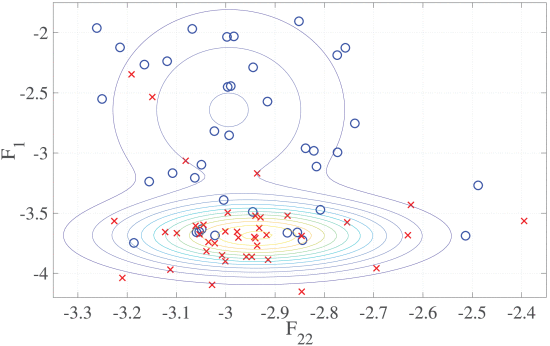
The common spatial pattern (CSP) method is a dimensionality reduction technique widely used in brain-computer interface (BCI) systems. In the two-class CSP problem, training data are linearly projected onto directions maximizing or minimizing the variance ratio between the two classes. The present contribution proves that kurtosis maximization performs CSP in an unsupervised manner, i.e., with no need for labeled data, when the classes follow Gaussian or elliptically symmetric distributions. Numerical analyses on synthetic and real data validate these findings in various experimental conditions, and demonstrate the interest of the proposed unsupervised approach.