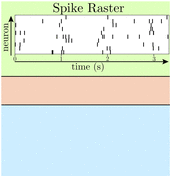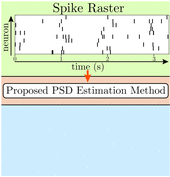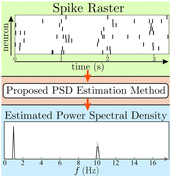
Characterizing the spectral properties of neuronal responses is an important problem in computational neuroscience as it provides insight into the spectral organization of the underlying functional neural processes. Although spectral analysis techniques are widely used in the analysis of noninvasive neural recordings such as EEG, their application to spiking data is limited due to the binary and non-linear nature of neuronal spiking. In this paper, we address the problem of estimating the power spectral density of the neural covariate driving the spiking statistics of a neuronal population, from binary observations. To this end, we consider a neuronal ensemble spiking according to Bernoulli statistics, for which the conditional intensity function is given by the logistic map of a harmonic second-order stationary process with sparse narrowband spectra. By employing sparsity-promoting priors, we compute the maximum a posteriori estimate of the power spectral density of the process from the binary spiking observations. Furthermore, we construct confidence intervals for this estimate by an efficient posterior sampling procedure. Our simulation studies reveal that our method outperforms the existing methods for extracting the frequency content of spiking data. Application of our method to clinically recorded spiking data from a patient under general anesthesia reveals a striking resemblance between our estimated power spectral density and that of the local field potential signal. This result corroborates existing findings regarding the salient role of the local field potential as a major neural covariate of rhythmic cortical spiking activity under anesthesia. In conclusion, our technique allows for analyzing the harmonic structure of spiking activity in a robust fashion, independently of the local field potentials. Other than its usage in the spectral analysis of neuronal spiking data, our algorithm can be applied to a wide variety of binary data, such as heart beat data, to obtain a robust spectral representation.