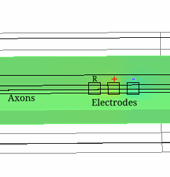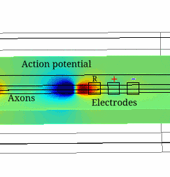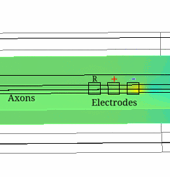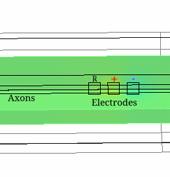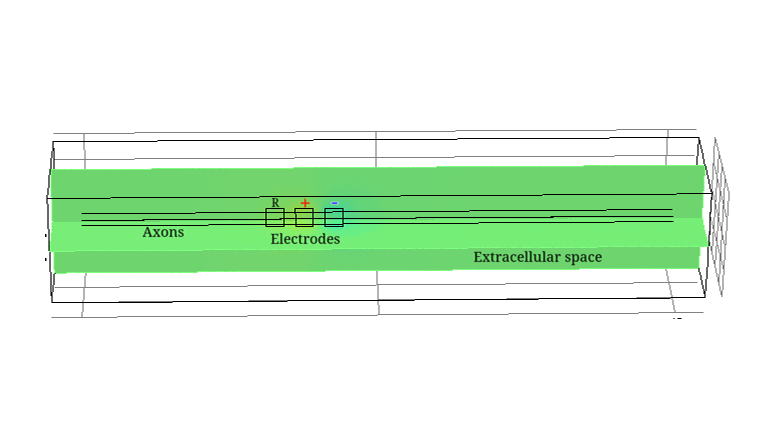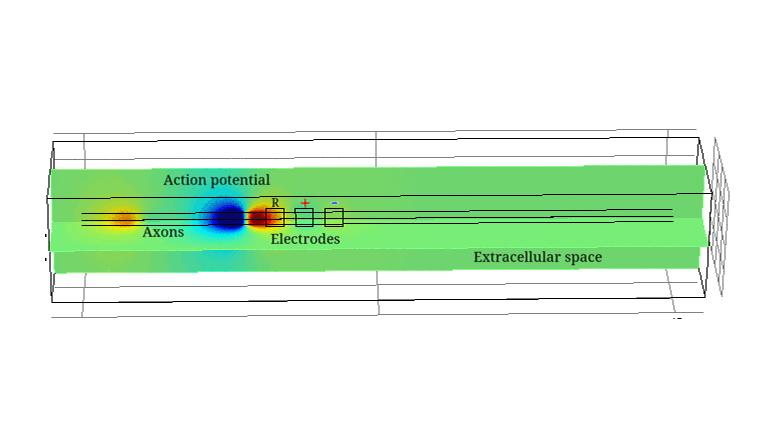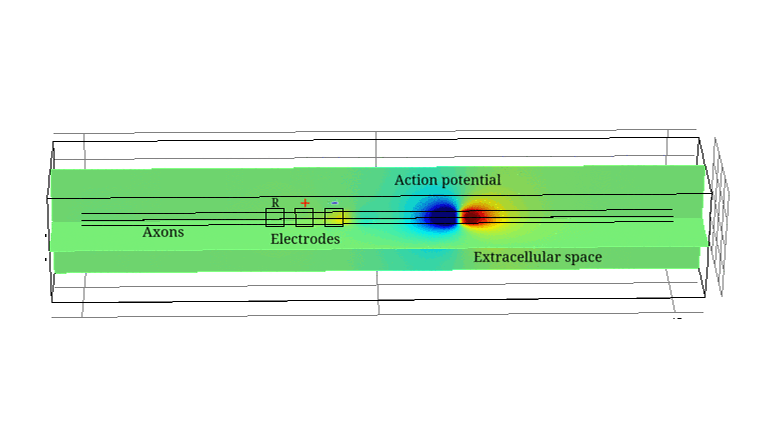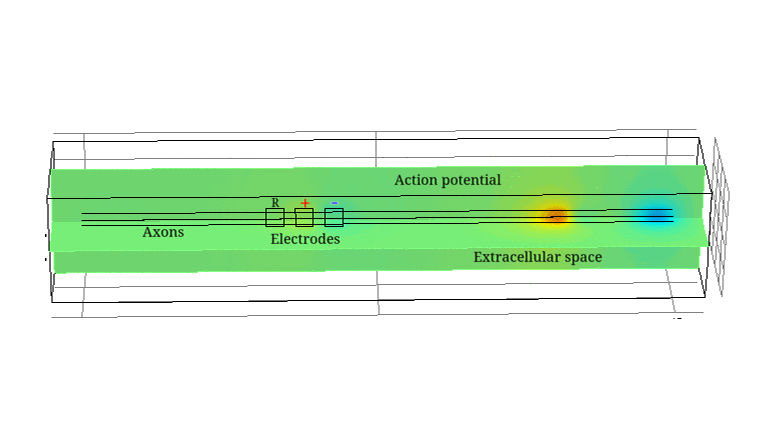
Electrical Impedance Tomography (EIT) is a technique able to image electrical impedance changes (dZ) in tissue by injecting alternating current and recording surface voltages. EIT has been shown to be able to visualise impedance changes related to neuronal depolarization over milliseconds in nerve or brain during activity. Electroceuticals is new field which aims to treat disease by electrical stimulation or block of autonomic nerves. EIT could be used to identify partial activity in fascicles in nerve and so avoid off-target effects by selective stimulation.
Neural impedance changes decrease with the size of the fibres and level of their myelination. Thus, imaging inside autonomic nerves consisting mainly of unmyelinated fibres requires maximising signal-to-noise ratio and therefore optimising imaging parameters. An accurate model of the unmyelinated nerve developed in this study helped to find these parameters as well as to validate data obtained in experiments in crab walking leg nerves.
In this study, realistic 3D models of unmyelinated fibres bi-directionally coupled with external space have been developed. The models included either Hodgkin-Huxley (HH) squid giant axon (single and multiple) or mammalian C-nociceptor.
The constructed models agreed with experimental data and allowed study of the variability of the impedance change with amplitude and frequency of the injected current, size and position of the electrodes, number of fibres, interaction between them and the model complexity. The models also provided the biophysical explanation of the observed dZ which are important for understanding the nature of experimental results.
The developed modelling approach serves as a basis for construction of a full model of the nerve, which will additionally include myelinated fibres and realistic morphology. Applications of such a model will include optimization of EIT for any nerves and study of the underlying causes of various nerve disorders.