Sander Land, Steven Niederer, Pablo Lamata, Nicolas Smith, King’s College London
Volume 62, Issue 3, Page: 939-947
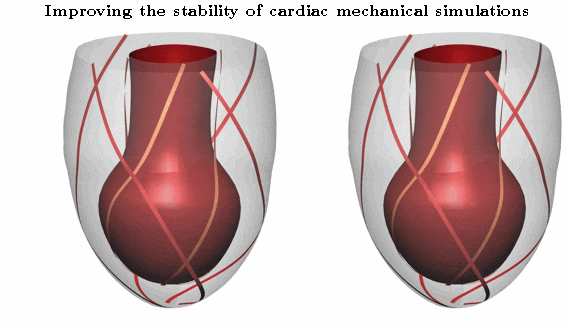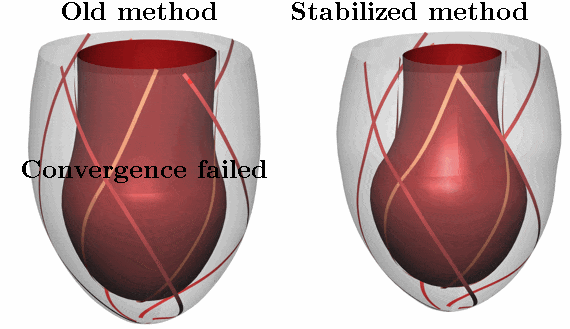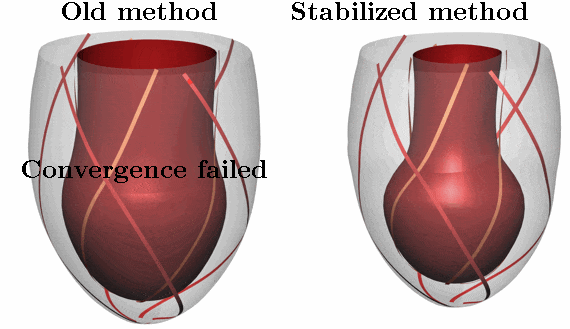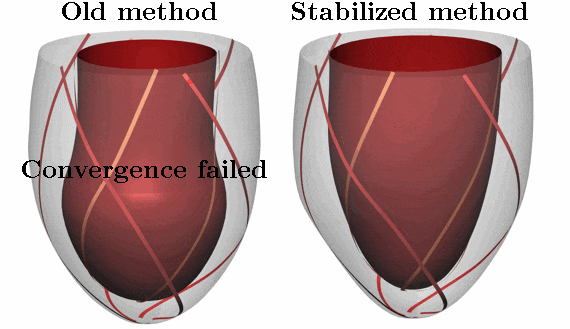
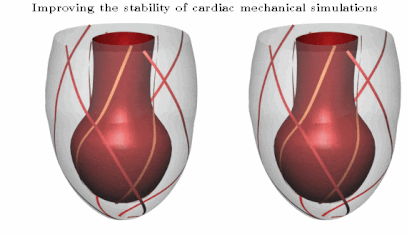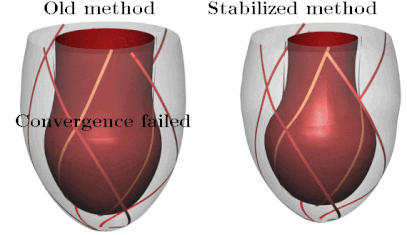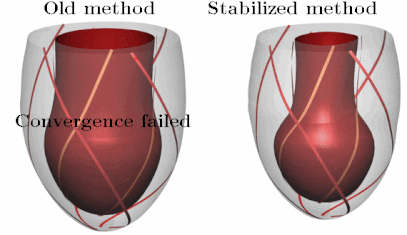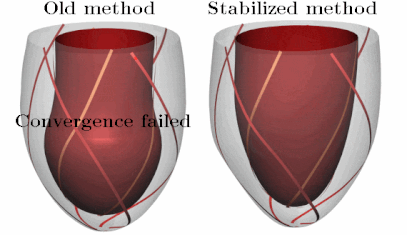
In the eld of cardiac modelling, the mechanical action of the heart is often simulated using nite element methods. These simulations are becoming increasingly challenging as the computational domain is customized to a patient’s anatomy and physiology. Our recent research into both cardiac resynchronization therapy and Takotsubo cardiomyopathy involves modelling complex heterogeneous deformation patterns with high mechanical stresses. When these situations with extreme stresses and irregular deformations are modeled, commonly used numerical methods can often fail to nd a solution. This lack of stability can prevent investigation of interesting parameter variations, which is required for using models to explore a range of hypotheses in studies of cardiac physiology, or when parameterizing novel models. In addition, these stability issues are a major obstacle in the use of models in a clinical context, where there are high standards for robustness. We have developed a novel numerical method that is straightforward to implement and which significantly improves the stability of these simulations. The method involves adding a compressibility penalty to the standard incompressible formulation of large deformation mechanics. The addition of this penalty improves the solution of the incompressibility constraint, and improves the eigenvalues of the Jacobian matrix, leading to a significant improvement in the ability of the Newton solver to find a solution. Additionally our method maintains the expected order of convergence under mesh refinement and has nearly identical solutions for the pressure-volume relations. We have tested our methods on a range of simple problems as well as simulations of both diastolic and systolic function using twenty personalized patient geometries. This new method is now driving our research into medically important problems.
More details on research by the Cardiac Electromechanics Research Group can be found at: http://www.cemrg.co.uk
Keywords: Cardiac Mechanics, Nonlinear Elasticity, Newton solver conver-gence