Computer modeling and simulation has become an important research tool in cardiac electrophysiology. Many fundamental mechanisms underlying cardiac arrhythmias were identified in or underpinned by computer simulations. High-fidelity state-of-the-art models require significant computational resources and often rely on supercomputers. Currently, these high computational demands limit the usefulness of cardiac computational models for direct clinical application (for example personalized simulations in digital twins) and for the generation of large-scale synthetic datasets for training in the setting of supervised machine learning.
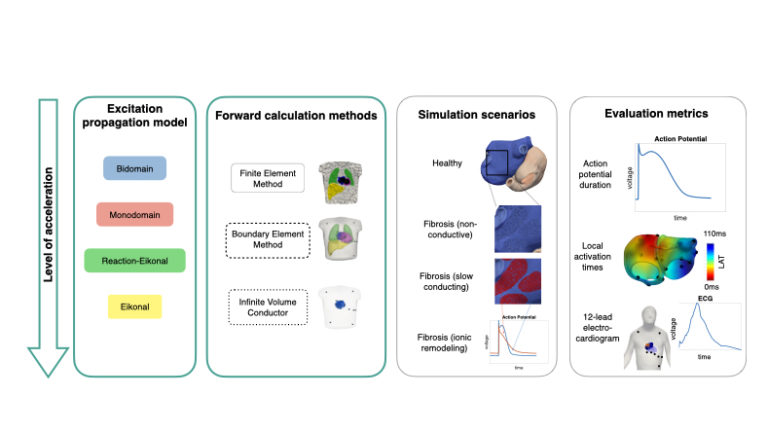
In this study, we systematically compare simpler but faster models of atrial electrophysiology to the accurate but computationally expensive bidomain model as an established reference. Both the model representing excitation propagation in the cardiac tissue as well as the methods to compute the P wave in the body surface electrocardiogram (ECG) are simplified and accelerated step by step. The results of the simplified multi-scale simulations are compared on the cellular level in terms of the action potential (reflecting the ion dynamics across the cell membrane), on the tissue level in terms of local activation times (reflecting the speed and path along which the excitation spreads across the atrial chambers) and the 12-lead ECG (reflecting the signals that can be easily measured non-invasively in clinical routine).
We found that all excitation propagation models faithfully represent the activation sequence of the realistic and heterogeneous bi-atrial model. For the repolarization sequence, the simplest model (plain Eikonal model) causes inaccuracies. Regarding the computation of the ECG for a given activation sequence, the boundary element method reproduced the gold standard well while the even simpler infinite volume conductor model overestimated the ECG amplitude in the precordial leads (close to the heart).
In conclusion, we showed that simulations of atrial activation sequences and ECGs can be notably accelerated to clinically feasible time frames at high accuracy by resorting to the Eikonal and boundary element methods.