Music has been prevalent in different societies and cultures since ancient times. It is an expression of human deeds, identity, wishes, understanding of the world, the culture and norms of each society, as well as interpersonal relations within the family and with the external world. The sounds different musical instruments produce affect human well-being. Moreover, music is also a human need, and, like language, it is another inborn communication means, very close to the basic physiological drives. [1]
Music therapy is a relatively frequent approach to several health problems nowadays, and it has its roots in ancient medicine, as was clearly showed by Liubov Ben-Noun in 2013 [1]. Moreover, music appears to be a truly natural, universal language that crosses all possible communication barriers. From our perspective and considering the physicomathematical foundations, music no doubt exhibits all the necessary ingredients to be readily interpreted as a subject within the bioengineering/biomedical engineering realm. As for the planets … let us leave their possible contribution in abeyance for the reader’s judgment after looking at what history teaches in this respect. Thus, this article intends also to explore the planetary musical links that go back at least to the 17th century. Quite interesting facts arise.
Johannes Kepler (1571–1630)
In Harmonices Mundi (The Harmony of the World, 1619), Kepler discusses harmony and congruence in geometrical forms and physical phenomena. In the final section, he gives an account of his famous and transcendental Third Law of Planetary Motion. In his day, true science was mixed with religion, mysticism, and philosophy, including unfounded concepts and beliefs.
Kepler, a German mathematician, astronomer, and astrologer, played a key role in the 17th-century scientific revolution: for example, his works provided a foundation for Isaac Newton’s theory of universal gravitation. Kepler was a mathematics teacher at a seminary school in Graz, Austria, where he became an associate of Prince Hans Ulrich von Eggenberg. Later, he became an assistant to the astronomer Tycho Brahe (1546–1601), and, eventually, he was made imperial mathematician to Emperor Rudolf II and his two successors, Matthias and Ferdinand II (1578–1637), all members of the house of Habsburg. Ferdinand II was, almost simultaneously, Holy Roman Emperor, king of Bohemia, and king of Hungary. His rule coincided with the Thirty Years War, and he aimed at restoring Catholicism as the only religion in the empire and suppressing Protestantism.
Kepler, meanwhile, was far more constructive and also taught mathematics in Linz, Austria. Additionally, he contributed to the field of optics, invented an improved version of the refracting telescope (the Keplerian telescope), and was mentioned in the telescopic discoveries of his contemporary, Galileo Galilei.
In Kepler’s time, there was no clear distinction between astronomy and astrology, but there was a strong division between astronomy and physics (a branch of natural philosophy). Kepler, as suggested previously, also incorporated religious arguments and reasoning in his work, motivated by the conviction that God had created the world according to an intelligible plan accessible through reason. Kepler described his new astronomy as celestial physics. Through it, he transformed the ancient tradition of physical cosmology by treating astronomy as part of a universal mathematical physics, whereas cosmology dealt only with the origin, general structure, and evolution of the universe.
Apparently, Kepler began working on Harmonices Mundi sometime around 1599, which was the year he anticipated a forthcoming text under the title De Harmonia Mundi (On the World’s Harmony). The content closely resembled that of Ptolemy’s Harmonica, but the new astronomy Kepler used, most notably the adoption of the elliptic orbits of the Copernican system, allowed him to explore new theorems. His celestial- harmonic relationships disregarded Pythagorean tuning as the basis for musical consonance; instead, he favored geometrical ratios. His intriguing proposal suggests a relationship between musical consonance and the angular velocities of the planets. The concept of musical harmonies within the spacing of the planets already existed in medieval philosophy. Musica universalis was a traditional philosophical metaphor that was taught in the quadrivium and was often referred to as the music of the spheres [2].
And what about the quadrivium? It was a set of subjects presented after the trivium curriculum was taught. Their use goes back to the sixth century. Both sets comprised the seven liberal arts, as opposed to the practical arts (medicine and architecture). The quadrivium consisted of arithmetic, geometry, music, and astronomy, and the trivium covered grammar, logic, and rhetoric. The quadrivium was intended to precede the study of philosophy (the liberal art par excellence) and theology (the highest knowledge to which humanity could aspire) [3].
While medieval philosophers spoke metaphorically of the music of the spheres, Kepler discovered physical harmonies in planetary motion. He found that the difference between the maximum and minimum angular speeds of a planet in its orbit approximates a harmonic proportion. For instance, the maximum angular speed of Earth as measured from the sun varies by a semitone (a ratio of 16:15)—from mi to fa—between aphelion and perihelion. Venus varies by only a tiny 25:24 interval (called a diesis in musical terms). Kepler explains the reason for Earth’s small harmonic range by stating, “The Earth sings mi, fa, mi; you may infer even from the syllables that in this our home, misery and famine hold sway.”
The celestial choir Kepler formed was made up of a tenor (Mars), two basses (Saturn and Jupiter), a soprano (Mercury), and two altos (Venus and Earth). Mercury, with its large elliptical orbit, was determined to be able to produce the greatest number of notes, while Venus was found to be capable of only a single note because its orbit is nearly a circle. Remember, the perihelion is the point in the orbit of a celestial body where it is nearest to its orbital focus. It is the opposite of the aphelion, which is the point in the orbit where the celestial body is farthest from its focus. At extremely rare intervals, all of the planets might sing together in perfect concord. Kepler proposed that this may have happened only once in history, perhaps at the time of creation. Quite an imposing, beautiful, even romantic thought! Take it, leave it, or regard it as a mere insignificant astronomical tale.
Kepler discovered that all but one of the ratios of the maximum and minimum speeds of planets on neighboring orbits approximate musical harmonies within a margin of error of less than a diesis (a 25:24 interval). The maximum and minimum speeds of Saturn (measured in terms of arc seconds seen from the sun) differed by an almost perfect 4:5 ratio (a major third). The extreme motions of Jupiter differed by a 5:6 ratio (a minor third in auditory space). The orbits of Mars, Earth, and Venus approximated the following harmonies: 2:3 for Mars; 15:16 for Earth, or the difference between mi and fa; and 24:25 for Venus. The orbits of Mars and Jupiter produced the one exception to this rule, creating the unharmonic ratio of 18:19. In truth, however, the cause of Kepler’s dissonance might be explained by the fact that the asteroid belt separates those two planetary orbits, as discovered in 1801, more than 170 years after the scientist’s death.
Kepler’s previous book, Astronomia Nova, related the discovery of the first two of the principles we know today as Kepler’s laws. The third law, which shows a constant proportionality between the cube of the semimajor axis of a planet’s orbit and the square of the time of its orbital period, is set out in Harmonices Mundi. No ordinary mind occupied that head, indeed! Some modern musical compositions either make reference to or are based on the concepts of Harmonices Mundi. Most notable among them are
- Laurie Spiegel’s Kepler’s Harmony of the Worlds (1977), an excerpt of which was selected by Carl Sagan for inclusion on the Voyager Golden Record launched aboard the Voyager spacecraft
- Music of the Spheres (an album released in 2008 by Mercury Records) by Mike Oldfield, an English musician and composer born in 1953
- Harmony of the Spheres, a cycle in five movements for mixed choir and string orchestra written in 2001 by Joep Franssens, a Dutch composer born in 1955
- American composer Philip Glass’s 2009 opera Kepler, a homage commissioned by the city of Linz, where the astronomer once lived [4].
What Modern Music Says
The Greek philosopher and mathematician Pythagoras of Samos (ca. 580–ca. 500 BCE) is credited with discovering that harmonic intervals correspond to unique whole-number proportions. Dividing the vibrating string of a musical instrument in the ratio 1:2 produces the interval we call an octave. Dividing a string in a 3:2 ratio creates the interval known as the fifth, producing the difference between do and sol. A fourth, the difference between do and fa, represents a 3:4 division of a string [5]. Today, we recognize that these musical intervals are produced by, in the case of an octave, doubling the rate of vibration of a string (say, from 200 vibrations/s to 400 or from 220 to 440). A fifth, the difference between do and sol, would be produced by two strings vibrating in the ratio of, for example, 200 to 300.
Each performer, when tuning his or her instrument, usually chooses a middle la, around 435–442 Hz; this is a question of taste, habit, or agreement with other musicians. A certain amount of dissonance is deemed necessary and even pleasant. Kepler rigorously investigated auditory space through experimentation. The followers of Pythagoras limited their musical system to the three intervals mentioned previously. But Kepler sought to determine all of the possible harmonic ratios for sound and to inquire as to their causes in the domain of geometry and mathematics (Figure 1).
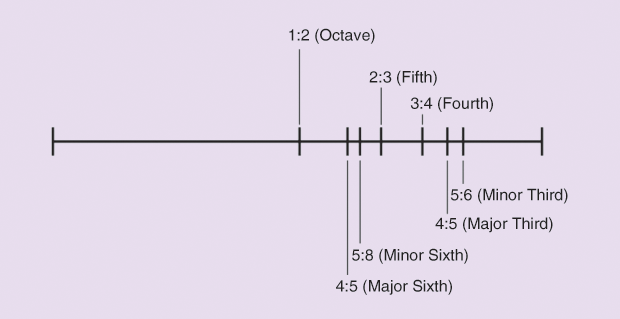
There is, however, a small discrepancy (called a syntonic comma, diatonic comma, or chromatic diesis) within an octave. It is a small interval between two musical notes, equal to the frequency ratio 81:80 (~21.51 cents, the cent being a logarithmic unit of measure used for musical intervals). Two notes that differ by this interval would sound different from each other, even to untrained ears, but would be close enough that they would more likely be interpreted as out-of-tune versions of the same note than as different notes. Without some system of tempering to adjust for these discrepancies, the commas would accumulate on an instrument based on equal steps, throwing off harmonies as one continued up the range. Tuning in equal temperament is the tuning of a keyboard instrument—as the piano, organ, or harpsichord—so that it may be played in all keys without further tuning. In music theory, the comma is the amount by which the Pythagorean major third (81:64, around 407.82 cents) is corrected to a just major third (5:4, around 386.31 cents). Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each. Typically, cents are used to express small intervals or to compare the size of comparable intervals in different tuning systems. The interval of 1 cent is too small to be noticed between successive notes [6].
Vincenzo Galilei (1520–1591), Galileo Galilei’s father and a musical theorist, championed a system of equal tuning that split the difference—the commas—to facilitate composition and performance on the piano. Kepler regarded this idea as simplistic and mistaken. He thought a more elegant system for tuning needed to be found. Just as planetary orbits were not based on perfect circles, he believed that the principles underlying harmony could not be reduced to musical atoms (cents) without sacrificing true consonance. The concept of atom was questioned in those days, including its possible (and scary) qualification as heresy.
Discussion
Music therapy is an actual medical fact, with many outstanding and demonstrated accomplishments. Unfortunately, it is not quantifiable as other medical practices more or less are, and it is by far much less predictable; only mere conjectures can be made. The bibliography abounds, but this is not the place to go further.
Planetary music, harmonies, and consonances appear on first sight to be obviously farfetched or at least debatable. Guillermo Boido [7] strongly questions such notions, calling them unfit and improper for a scientist, not even worth mentioning. Other historians over the years have also shared this view, accusing Kepler of fanatism, superstition, or even fevered thoughts. Nonetheless, the idea is intrinsically beautiful and, being based on real astronomical facts, may be accepted with a grain of pleasure.
Daniel Pickering Walker (1914–1985), an English scholar and historian, observed that Kepler’s celestial harmonies are unique in several respects, especially because they are real but soundless. Kepler examined the ratios between the fastest or slowest speed of a planet and the slowest or fastest speed of its neighbors and discerned harmonies in each case, with discrepancies smaller than a diesis, or 24:25, the smallest harmonic interval a human ear can detect. The only interval with a deviation from harmony larger than 24:25, Kepler found, was the diverging motion of Mars and Jupiter. As mentioned earlier, the asteroid belt was discovered in 1801.
It is appropriate to mention the enharmony concept—the ability to write the same pitch in more than one way. For example, F# and G♭ are enharmonic sounds. The idea closely relates to the notion of the diesis [8]. In classical Western music, a diesis (difference, in Greek) is a very small musical interval, usually defined as the difference between an octave (in the ratio of 2:1) and three justly tuned major thirds (tuned in the ratio of 5:4), equal to 128:125 or about 41.06 cents. In 12-tone equal temperament (on a piano, for example), three major thirds in a row equal an octave, but three justly tuned major thirds fall quite a bit short of an octave, and the diesis describes the amount by which they are short. For instance, an octave (2:1) spans from C to C’, and three justly tuned major thirds (5:4) span from C to B# (namely, from C to E to G# to B#). The difference between C and C’ (2:1) and C and B# (125:64) is the diesis (128:125). Notice that this coincides with the interval between B# and C’, also called a diminished second. The diesis is a comma. The 128:125 comma is also known as the lesser diesis, as opposed to a wider comma (648:625), known as the greater diesis. As shown in Figure 2, in the quarter-comma meantone tuning system (a tuning system in which, by definition, major thirds are justly tuned), the diminished second coincides with the diesis.
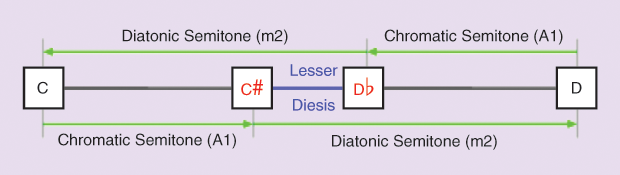
Going just a little deeper into music theory and for the sake of melodies, an enharmonic scale is an imaginary gradual progression by quarter tones. The enharmonic scale uses dieses nonexistent on most keyboards, because modern standard keyboards have only half-tone dieses. More broadly, an enharmonic scale is a scale where there is no exact equivalence between a sharpened note and the flattened note with which it is enharmonically related, such as in the quarter-tone scale. As an example, F# and G♭ are equivalent in a chromatic scale (the same sound is spelled differently), but they are different sounds in an enharmonic scale.
The patient reader is free to judge this mixed musically based essay according to his or her reactions, feelings, and previous background. Finally… is all of this biomedical engineering? Perhaps…
References
- L. Ben-Noun (Nun). (2015, Sept. 15). Music therapy in the Bible. [Online].
- Musica universalis. [Online].
- Quadrivium. [Online].
- Harmonices Mundi. [Online].
- M. E. Valentinuzzi and N. E. Arias, “Human psychophysiological perception of musical scales and nontraditional music,” IEEE Eng. Med. Biol. Mag., vol. 18, no. 2, pp. 54–60, 1999.
- Syntonic comma. [Online].
- G. Boido, News from the Planet Earth: Galileo Galilei and the Scientific Revolution, (in Spanish). Buenos Aires, Argentina: AZ Editora, 1996.
- Diesis. [Online].


