A History of the Convolution Operation

[accordion title=”About Convolution and Alex”]
Either write something worth reading or do something worth writing.
— Benjamin Franklin (1706-1790)
Math and music are two areas that have attracted my attention ever since I was in elementary and high school. No doubt, a couple of teachers influenced me, and for sure my father did too as he often spoke with admiration of the great mathematicians and musicians. Besides, the two areas are linked: both show the beauties of striking and magnificent consonances and dissonances. Thereafter, already at the engineering school of the University of Buenos Aires, another well-versed mathematician, Juan Carlos Vignaux (1893–1984), led me with enthusiasm into deeper and more powerful concepts and tools. Convolution soon caught my interest and made me smile with the pleasing description of a visiting guest function that turns around and greets the host function. Isn’t that a beauty? Not long after, many times I had to use the operation as a mere applied electronics engineer calculating transfer functions, often bouncing my head against a wall when the integrals became too thorny or when the Laplace transform table did not consider the fancy function for which I was looking.
I never bothered much to find out who was the owner of the brain that left us with such a superb inheritance until, many years later, the history of science and technology began to call my wits. Since the IEEE Pulse “Retrospectroscope” column was placed in my hands by its kind editors back in 2011, I have been like a hunter in a permanent search for adequate subjects to dig into their respective pasts, and convolution returned to my memory. Swiftly and with pleasure, I started to probe into my files, old notes (I even called a former colleague, a math professor), and ended up navigating through our all-mighty Internet. At one point, and already having a coarse preliminary draft, I ran across this website, realizing that the right guy was at hand, Alejandro (Alex) Domínguez, verifying once more what Matthew (7:7) stated ages ago, “Ask, and it will be given you; search, and you will find; knock, and the door will be opened for you.” I knocked at the door and asked Alex to write the knowledgeable article you readers have here telling us the origins of convolution. We both hope it meets what Benjamin Franklin wisely stated in the quote at the beginning of this column.
Let me introduce to you Alejandro Domínguez, who was born in Mexico City, Mexico, on 18 April 1960. He received his B.Sc. degree in physics from the Universidad Nacional Autónoma de México in 1984, his master of science degree in physics from the same university in 1989, and his Ph.D. degree in applied computing and mathematics from Cranfield University, Bedford, United Kingdom, in 1992. From 1992 to 2000, he was with the Fundación Arturo Rosenblueth, Mexico City. From 2000 to 2001, he was an invited professor at the Universidad Politécnica de Cartagena, Murcia, Spain. From 2001 to 2003, he was again with the Fundación Arturo Rosenblueth, and since 2003, he is with the Universidad Tecnológica de México, Mexico City, where he is currently the corporate director of postgraduate studies. His research in mathematics has been concerned with the history associated with the Fourier integral transform and the convolution operation, as well as using both operations for solving problems associated with classical physics and computer-aided design. He was awarded for his academic work by Cranfield University (1992), the Universidad Tecnológica de México (2010), and the Centro Nacional para la Evaluación de la Educación Superior, Mexico (2014). No doubt, he is the right person to speak about this subject.
—Max E. Valentinuzzi
maxvalentinuzzi@arnet.com.ar
[/accordion]
For applied mathematicians, physicists, and engineers, there is no doubt of the usefulness and applications of the continuous convolution operation (CCO). The number of applications is so large that trying to name and count them would take a long time. Despite this fact, almost none of the modern books that discuss the theory and applications of the CCO report its origin. The main reason for this lack of background information is that the CCO is usually discussed in books where the chief topic is the theory and applications of an integral transform, mostly Fourier’s or Laplace’s. This has also been the case in much of the earlier literature, except in a small number of documents, i.e., three books [1]–[3] and two electronic documents [4] and [5].
In a series of remarks throughout the book as well as a discussion at the end, [1] provides some historical notes. Although many of the comments are limited to a note referring to other sources, [2] gives brief historical notes, which appear in two subsections of Appendix C (pp. 364–365). In [3], the second half of the chapter “Mesure de Harr; Convolution” is dedicated to historical remarks; however, many of them are quoted without referring to a specific source.
Concerning the electronic sources, the contribution by Miller [5] provides few annotations about the history of the CCO, and some of them are inaccurate. My paper [4] was the first attempt to describe this history, and is the main source for this article. Nevertheless, it contains a certain number of inaccuracies because I based some part of my research on the corresponding information stated by other authors. With the access to the Internet and to specialized Web pages, it has been possible to consult and exhaustively verify the sources. Thus, 23 years later, it is possible to develop a more precise description of this history.
As in the original paper [4], two important remarks must be made before proceeding with this article. First, the history of the CCO described herein is far from being complete; in fact, the reader may find there are no comments about the work of some authors. Second, there is no intention to assess or criticize the events or facts; the information provided is more descriptive than critical.

The Birth of the COO

It was the 1760s when the Swiss mathematical genius Leonhard Euler (1707–1783) suffered complete blindness, but this illness did not prevent him from contributing to mathematics. In fact, in those years, he wrote a memorable book about integral calculus and the solution of differential equations (DEs) by certain definite integrals [6]. In Chapter X of this book, and specifically in problem 131 (section 1049, p. 248), he studied the solutions of ­second-order partial DEs of the form

A first and simple case of this solution is K(u) = u and Q(x) = x and a second case is K(u) = -u and Q(x) = x. Euler studied the first case in [7], which is the first source in which the correlation operation is used exhaustively in statistical applications and related to convolution. Concerning the second case, (1) results in a particular form of the mathematical operation show the reason for this paper

However, it seems that Euler did not study (2) in particular, but he did study the case when Q(x)= x and K(u) is any other function [6, p. 251].
A more general form of (2) appears “naturally” in the solution of DEs by integral transforms (like Fourier or Laplace transforms) related to computational fluid dynamics, electrical engineering, heat conduction, signal and image processing, linear acoustics, mechanical engineering, optics, probability and statistics, radiotherapy, spectroscopy, and viscoelasticity. Specifically, for the given two complex-­valued suitable functions f and g of a real or complex variable argument, the following expression is more general than (2):

Here, l may be either an interval of integration (a, b) if α is a real variable or a curve if α is a complex variable. For the first instance, the three most common cases are the following, where – ∞ < a < b < ∞:
L
From a graphical point of view and α being the main variable, this operation consists of the mathematical process that can be interpreted graphically by folding the argument of function g, translating the argument of function g, multiplying the resulting function g by function f, and integrating that multiplication [2, p. 232]. Moreover, this interpretation and its graphical representation possibly appeared for the first time in the same book in its first edition in 1942.
Therefore, the operation is in some sense the “revolving” of one of the input functions with the other one. Particularly in mathematics, physics, and related areas, the verb commonly used to designate such a revolving is “to convolve.” This verb comes from the Latin words con and volve˘re, which mean “together” and “roll up,” respectively; thus, convolve means “roll up together.” Accordingly, the action of convolving is called convolution. This is why (3) is usually known today as the CCO, or simply convolution, although it has been given many other names in the past, as discussed in the section “Names of the CCO.”

Historical Development of the COO

The task of tracing back the history of the CCO is not an easy one since it requires reviewing and verifying information contained in a number of books and papers. In some cases, the information provided is not exact, while in others, it comprises only some comments with no references. In any case, tracing back these occurrences, true or supposed, is the main goal of this section. Fortunately, there is at least a starting point: the book by Euler [6, pp. 230–255].
An example of a supposed occurrence is attached to the French mathematician Pierre-Simon Laplace (1749–1827). In fact, Miller [5], in the entry “Convolution,” makes the following statement:

Expressions that would now be described as “convolutions” appear in Laplace’s earliest work on sums of independent random variables, “Mémoire sur l’inclinaison moyenne des orbites des comètes, sur la figure de la terre et sur les fonctions,” Mémoires de l’Académie Royale des Sciences de Paris, Savants Étrangers, vol. 7, pp. 503–540, 1773.

Nevertheless, after reviewing this memoir, no trace of the CCO is found. Miller also notes that:

A succession of French and Russian mathematicians followed Laplace and used convolutions without, it seems, evolving a name for them. See A. Hald History of Mathematical Statistics from 1750 to 1930 (1998).

However, Hald’s book states that Laplace indeed used the CCO for solving the problem of finding the distribution of the mean, and this occurred on p. 478 of a memoir written in 1778 and published in Mémoires de l’Académie Royale des Sciences de Paris in 1781. Thus, the citation given by Miller about Laplace’s work seems to be inaccurate.
This memoir by Laplace has been the inspiration of many applied mathematicians and engineers for developing many other theories and results. This is the case of the work about differences and series published in a book in 1800 by the French mathematician Sylvestre François Lacroix (1765–1843). Therein, the CCO appeared in an application regarding the summation of series by definite integrals. It is worth mentioning that this is perhaps the first time the CCO appeared in its more general form, as in (3). Incidentally, the German mathematician Heinrich Friedrich Karl Ludwig Burkhardt (1861–1914) cited the work by Lacroix in a footnote that appeared in [8, p. 400].
At the beginning of the 19th century, a young mathematician interested in the application of mathematics to physical phenomena started to write a memoir called Théorie de Mouvement de la Chaleur Dans les Corps Solides, which was later part of his celebrated book first published in 1821–1822, Théorie Analytique de la Chaleur. This mathematician is, of course, Jean Baptiste Joseph Fourier (1768–1830) [9]. In this book, the CCO appeared in section 265 [9, pp. 233–234]:

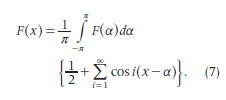
Fourier’s book is the first in which the CCO appeared a number of times (see, e.g., Chapter IX).
Two contemporaries of Fourier were the French mathematicians Augustin Louis Cauchy (1789–1857) and Siméon Denis Poisson (1781–1840). Cauchy made use of a number of CCO expressions in a long memoir on the theory of propagation of waves presented to l’Académie des Sciences de l’Institut de France and submitted to the 1815 competition for the award of mathematical analysis. Regarding Poisson, the CCO first appeared in his memoir on the theory of waves published in 1816.
Poisson employed the CCO in his subsequent papers. For example, in an 1826 memoir about the magnetism in movement, the CCO appeared a number of times. Concerning this memoir and the use of the CCO, Gardner and Barnes write [2, p. 364]: “The treatment of this paper leads to the supposition that these ideas were already known.”
In fact, in the 1820s, the idea of CCOs was quite common in the applied mathematics environment. For example, an expression of the type given by (2) appeared in the solution of certain integral equations derived from definite problems in physics. This is the case of the integral equation that appeared in the problem of tautochrone curves, which was solved by the Norwegian mathematician Niels Henrik Abel (1802–1829) and published in two papers in 1823 and 1826.
At the end of and after the 1820s, the use of the CCO became more common in papers related to pure and applied mathematics. Table 1 chronologically lists references of these uses cited in [1]–[5].
[accordion title=”Table 1. Some Uses of the CCO Over Nearly a Century”]

Year	Uses of the CCO
1829	The German mathematician Peter Gustav Lejeune Dirichlet (1805–1859) used the CCO to study the convergence of Fourier series.
1831, 1834, and 1841	Cauchy used the CCO in a in a long article presented to the Academy of Science of Turin in 1831. He also gave several reformulations of the CCO in his papers in 1834 and 1841. Of course, Cauchy’s CCO formulation is none other than the so-called Cauchy integral formula in the theory of functions of complex variables.
1834	The French mathematician Jean Marie Constant Duhamel (1797–1872) used the CCO to explain the theory of vibrations of an arbitrary points system. Gardner and Barnes [2, p. 364] cited another memoir (1833) where Duhamel used the CCO; however, after reading it, there is no evidence of such a CCO.
1843 and 1863	The French mathematician Pierre Alphonse Laurent gave the next important application of the Cauchy integral formula (connected with the CCO) in his derivation of his celebrated series expansion, whose coefficients are of the CCO type. His results occurred in a reported but unpublished paper in 1843. The complete paper was published 20 years later, nine years after his death.
1848	The German mathematician Oscar Xaver Schlömilch (1823–1901), in his book about mathematical analysis and Fourier series and integrals, used the CCO to define fractional derivatives and to evaluate a certain type of definite integrals related to Gamma function.
1848	The German born physicist Franz Ernst Neumann (1798–1895) expressed the associated Legendre polynomials of the second kind by means of the one of the first kind by using the CCO.
1854	The Hanover-born mathematician Georg Friedrich Bernhard Riemann (1826–1866) used a CCO to investigate the convergence of Fourier series. As a matter of interest, the CCO used by Riemann was similar to that given by Dirichlet in 1829 in his work about this theory.
1867 and 1887	There are supposed uses of the CCO by the Russian mathematician Pafnuty Lvovich Tchébychef (1821–1894). Gardner and Barnes cited that “Tchebycheff made implicit use of convolution in an 1867 paper […] and an explicit use in an 1887 paper […]” [2, p. 364]. However, after a revision of the corresponding papers, there is no evidence of an either implicit or explicit use of the CCO. Due to this fact, both supposed uses of the CCO by Tchébychef still remain as an enigma. As a matter of interest, the surname Tchébychef appears in the literature with different spellings, such as: Tchebychef, Chebychev, Tschebyscheff, Tchebysheff, and Tchebichef.
1874	The Austrian physicist Ludwig Boltzmann (1844–1906) used the CCO several times to solve problems in elasticity and ­electrostatics.
1877	The British physicist John Hopkinson (1849–1898) invoked Boltzmann’s method and used the CCO to solve a problem about the dielectric properties of different glasses.
1884	The Russian mathematician Nikolay Yakovlevich Sonin (1849–1915) used the CCO for generalizing an Abel’s integral equation.
1884	The French mathematician Matthieu Paul Hermann Laurent (1841–1908) [not to be confused with Pierre Alphonse Laurent (1813–1854)] defined fractional derivatives by means of the CCO.
1885	The Westphalian-born mathematician Karl Theodor Wilhelm Weierstrass (1815–1897) used the CCO for approximating a continuous function.
1892	The Italian engineer, sociologist, economist, political scientist, and philosopher Vilfredo Federico Damaso Pareto (1848–1923) used the CCO for generating a certain class of functions defined by Abel.
1892	The Italian mathematician Vito Volterra (1860–1940) started to use the CCO and correlation in relation with transformations of Lamé´s equations. After this paper, the use of the CCO became common in most of his papers. They were the basis for developing his theory of integral equations.
1896	The Finnish mathematician Robert Hjalmar Mellin (1854–1933) used the CCO for solving differential equations. After the work by Euler, his work is perhaps the most complete one about the use of the CCO for solving differential equations.
1899	The Swiss mathematician Charles Cailler (1865–1922) used the CCO for solving a certain DE with linear coefficients, which he called the “Laplace equation.”
1899	The French mathematician Félix Edouard Justin Émile Borel (1871–1956) made use of the CCO for proving that the product of two absolutely summable series is also absolutely summable. His results were closely related to the so-called convolution theorem, whose history is described in the section “Main Theorems and Computation of the CCO.”
1905	The British mathematician Ebenezer Cunningham (1881–1977) used the CCO to extend Borel’s results about summability of series and applied it to finding solutions of differential equations.
1905	The British mathematician Harry Bateman (1882–1946) proved that the CCO of two Bessel function of different orders is proportional to the Bessel function with order the sum of the two previous orders.
1905	The Dutch astronomer Jacobus Cornelius Kapteyn (1851–1922) derived many integral properties of Bessel functions by using the CCO.
1908	The British mathematician Thomas John l’Anson Bromwich (1875–1929) made use of the CCO for reformulating Borel’s results about summability of series.
1907	Despite the many occurrences and uses of the CCO, none of the previous authors made a complete study of it. The earliest one is, perhaps, that made by the Austrian-born mathematician Salvatore Pincherle (1853–1936) in connection with the solution of the complex integral equation where P > 0 and k(z) and g(z) are given functions, while f(z) is unknown. Pincherle succeeded in the solution of this CCO using as tool the Laplace transform. His results and of other authors are summarized in [1, Ch. 17]. These results are the basis for the deconvolution method established in [10].
1920	The Chilean-born British mathematician Percy John Daniell (1889–1946) defined the Stieltjes-Volterra Products as a CCO of the type

[/accordion]
After 1920, the CCO entered as a multiplication operator in the theory of groups developed by the German mathematician Hermann Klaus Hugo Weyl (1885–1955). The collective of (mainly) French mathematicians who used the pseudonym Nicolas Bourbaki (officially known as the Association des collaborateurs de Nicolas Bourbaki), noticed the importance of this theory in future applications of the CCO [3, p. 295], mainly in the development of the theory of normed algebras by the Ukrainian mathematician Israil Moiseevic Gelfand (1913–2009), as well as in the foundations of the theory of distributions established by the French mathematician Laurent Moise Schwartz (1915–2002) in 1950–1951.
In Bourbaki’s book, it is also pointed out that the measure theory developed by the Hungarian mathematician Alfréd Haar (1885–1933) and the CCO theory had become essential tools for exploring ways of algebraizing some processes of mathematical analysis (e.g., differentiation and integration) [3, p. 295].
This idea of algebraizing was not new at the time. In fact, it had been present in the applied mathematics environment since the time of the German philosopher and mathematician Gottfried Wilhelm von Leibniz (1646–1716). His ideas were later explored and developed by many other applied mathematicians, physicists, and engineers. For example, in 1950, the Austrian–Hungarian Empire-born mathematician Jan Geniusz Mikusin’ski (1913–1987) published a paper and three years later a book where he developed a method for algebraizing the CCO.
More can be said about tracing the development of the CCO. In fact, if the literature associated with the CCO were studied in detail, the following could be deduced:

1. The CCO appeared naturally during the solution of problems related to physics or mathematics.
2. The CCO did not receive any special treatment until the 1890s.
3. Since its beginnings, the CCO has been closely linked with integral transforms, either finite (as the coefficients of Fourier series) or infinite (as Fourier or Laplace transforms). To visualize this statement clearly, the reader is invited to look at any book of integral transforms, such as Fourier’s and Lapalace’s.

Names of the CCO

Giving something a name is the most important way of identifying it. However, sometimes names do not come about until there is sufficient interest. This is the case for the CCO. The first name given to integrals of the type given by (2), with n being negative, was “Euler transform.” Of course, Euler did not give his own surname to these integrals; thus, who coined this name? The answer to this question is found on page 415 of an 1897 handbook about DEs written by the Hungarian-born mathematician and physicist Ludwig Schlesinger (1864–1933), who coined this name in imitation of the Laplace transform.
Since “Euler transform” only refers to a particular type of integrals, it cannot be appropriate for designating the CCO in general. In the meantime, in 1899, the German mathematician Charles Cailler (1865–1922) gave the name résultante (resultant) to the result of performing the CCO in a note about the Laplace’s DE and Abel’s formula.
The name for the operation came about some years later, and it is due to the Italian mathematician Samuel Giuseppe Vito Volterra (1860–1940). In fact, in a 1910 paper concerning a general question on integral and integrodifferential equations, he wrote that given two finite and continuous functions F1(x,y) and F1(x, y) the “composition” (composizione) of them is defined as

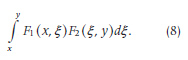
He went further and said that and are the “components” (componenti) while the integral is the “resultant” (risultante). Of course, the operation of “composition” corresponds to a more general type of operation, where the CCO given by (5) is only one instance when F1(x, y) = F1(y-x) and F2(x, y) = F2(y – x). Consequently, the first general name given to the CCO itself, and not to its result, was that of “composition,” later renamed by Volterra as “composition of the first type” (composition de première espèce).
In the same paper, he defined the “composition of the second type” for two continuous and finite functions  F1(x, y) and F2(x, y) as

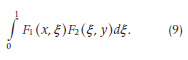
Later, in his lectures about permutable functions delivered at Princeton University in 1912 and published in 1915, the “composition of the second type” was generalized and defined as

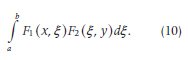
Of course, this expression is more general than (4).
A slight modification of the name composition has also been used in the French literature: produit de composition (composition product). This occurred in a 1947–1948 paper about theory of distributions and Fourier transform written by Laurent Schwartz.
In German literature, the preferred name was faltung, as can be verified in [1, p. 157]. The German mathematician Gustav Doetsch (1892–1977) attached this name to the CCO in 1923 in his paper about integrodifferential equations of faltung type. In the period immediately after the appearance of this paper, many American authors favored the name faltung. This is supported by the following quotation taken from the American mathematician Norbert Wiener (1894–1964) in his book The Fourier Integral and Certain of Its Applications:

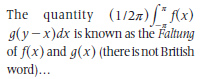
On the other hand, as is reported in the entry “Convolution” of the 2009 edition of the Oxford English Dictionary, the name convolution appeared as early as 1934 in a paper about analytic convolutions of Bernoulli distributions written by the Budapest-born Aurel Friedrich Wintner (1903–1958). He coauthored another paper about distribution functions and the Riemann zeta function (published in 1935) where the concept of convolution appeared again. In it, there is an interesting fact about the relation of the CCO and the Fourier transform:

The proper method in dealing with distribution functions and their convolutions (“Faltungen”) is the method of Fourier transforms, first applied systematically by [Paul Pierre] Levy in his book on the calculus of probability.

The book by the French mathematician Paul Pierre Lévy (1886–1971) cited is Calcul des Probabilités, published in 1925.
In 1937, the name convolution was considered by Doetsch as the most appropriate translation of the German term faltung [1, p. 157]. Gardner and Barnes also used this name around 1942 in their book for referring to an integral of the type given by (3), as is established in the following quotation [2, p. 228]:

The process expressed by the integral will be called convolution in the real domain, or real convolution, and the functions […] will be said to be convolved.

The process of folding in the graphical interpretation of the CCO agrees with the translation to English of the German word faltung, which is indeed “folding.” Moreover, it agrees with the definition given in the Oxford English Dictionary. According to it, the word convolution is close to the action of folding, and according to its etymological roots it relates with the action of “rolling up together,” as mentioned previously.
Nowadays, the use of the name convolution has become common in the literature. However, other not-so-famous names have also been attached to it. For example, in a paper originally published in 1958 in Volume XXXVII of The Bell System Technical Journal and one year later in their book about the measurement of power spectra from the point of view of communications engineering, Ralph Beebe Blackman (1904–1990) and John Wilder (1915–2000) Tuckey pointed out:

Convolution is often called by a variety of names such as Superposition theorem, Faltungsintegral, Green’s theorem, Duhamel’s theorem, Borel’s theorem, and Boltzmann-Hopkinson theorem.

But Blackman and Tuckey gave no citations to this quotation. This is, perhaps, the origin of a similar paragraph quoted by the Australian electrical engineer Ronald Newbold Bracewell (1921–2007) in his book related to the Fourier transform and its applications.
The names “(weighted) running mean,” “smoothing,” “blurring,” “scanning,” and “smearing” come from the statistical and analytical properties of the CCO and will not be discussed here.

A Star is Born: Notations for the CCO

Concerning the notations for the CCO, Volterra gave the first one in his aforementioned 1910 paper. He denoted the resultant function (funzionerisultante) of the composition of the first type of two finite and continuous functions F1(x,y) and F2(x,y), given by an expression such as F1F2(x,y). He also mentioned that if no confusion exists with the product of the two functions, a simpler notation is F1F2.
In the same paper, he introduced a double star over the functions to denote the composition of the second type, as defined by (9). That is,
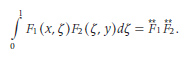(11)
Of course, the same notation was used for the composition of the second type defined by (10).
In 1912, in his lectures on line functions delivered at Sorbonne University and published one year later, Volterra used the single star over functions to denote the composition of the first type: F1*F2*(x,y) or F1*F2*. He went further with this notation and said that if F1 = F2 = F, then F1*F2* = F* F* = F*^2.
It seems that Volterra was not pleased with the single-star notation, and, in the same year, when he delivered a set of lectures at Princeton University concerning the theory of permutable functions (published in 1915), he added a third one: the square bracket notation [f, Φ].
However, not all authors followed the star or bracket notations used by Volterra. In fact, the Chilean-born British mathematician Percy John Daniell (1889–1946) used a “dot notation” in a conference delivered in 1920 at the International Congress of Mathematics in Strasbourg (France) and concerning Stieltjes-Volterra products

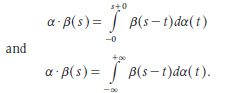
Over the years, a particular kind of combination of the single-star notation and the dot notation began to arise. This notation is the one used today in literature, namely, F1 * F2 (t). This notation appeared for the very first time in the aforementioned 1923 paper by Doetsch about integrodifferential equations of faltung type. Doetsch also used two variations of this notation: in [1 p. 161], he denoted (5) as  to be distinguished from the integral with infinite limits, (6), which he denoted as  These two notations seemed difficult to write and then rapidly disappeared from the literature.
The single-star notation defined by Volterra in 1912 survived with some modifications in position suggested by the dot notation defined by Daniell in 1920, which results in defining

Notice that this notation is concise, visible at one glance, and rapidly written. Though, a question arises: Why didn’t Volterra’s single-star notation survive? This question does not have an easy answer; however, it can be said that because the CCO is a binary operation (as in the case of addition and multiplication), then the symbol for denoting it should be in an infix position (as are the symbols “+” and “×”). This seems to be the best option.

Main Theorems and Computation of the CCO

Given a binary operation, it is natural to ask about its existence and the commutative properties. To answer these questions, notice that the CCOs given by (4) and (5) are particular cases of (6). In fact, (4) is obtained if one of the input functions is defined over a finite interval (a,b). Similarly, (5) is obtained from (6) if both functions are defined over the positive real line. With this in mind, what are the conditions for the existence of (6)? The Austrian–Hungarian mathematician Salomon Bochner (1899–1982) gave this answer by establishing the very first sufficient existence condition on pages 54–56 of his book Lectures on Fourier Integrals, written in German and published in 1932. Surprisingly, this condition says that for the existence (6), it is sufficient that the entering functions be absolutely integrable over all of the real line.
This condition is quite important for determining the validity of the commutative property. In fact, if at least one of the entering functions is not absolutely integrable over all of the real line, then the commutative property does not hold. A couple of counterexamples were presented to the scientific community in 1990 [11], almost 60 years after the publication of the book by Bochner!
On the other hand, another important theorem related to the CCO is the so-called convolution theorem. In general, the ­theorem establishes that the Laplace transform of the CCO (5) is the product of the Laplace transform of each input function. A similar result holds for (6) when the integral transform is the Fourier transform. In both cases, it is difficult to determine when both theorems appeared for the very first time. However, it can be said that the convolution theorem for (5) appeared in 1899 in Borel’s memoir about divergent series. For the case of (6), the convolution theorem appeared in the 1920 conference by Daniell about Stieltjes–Volterra products. In it, Daniell defined the convolution of any two measures over the real line, and then he applied the two-sided Laplace transform obtaining the corresponding convolution theorem. From it, he implied the result for the Fourier transform.
The importance of convolution theorems is that they allow computing the corresponding CCO indirectly. In fact, the CCO equals the inverse integral transform (either Laplace or Fourier) of the product of the integral transform (either Laplace or Fourier) of each input function. This fact simplifies the computations, since the direct calculation of the CCO is especially difficult for the case in which one or the other function is zero and discontinuous over various intervals of the argument. Thus, the problem arises in finding the appropriate limits and integrands associated with the integrals.
David E. Cartier defined a method to solve this problem in a paper published in 1975 and named “Mirror, Mirror on the Wall…Convolution Isn’t Hard at All.” The subtitle of his paper shows the essence of such a method: “Graphical Solutions Work Only for Simple Functions. A Piecewise Linear Method Can Work for All.” The basic idea is to use the expressions that define f and g, which are piecewise continuous, to create an (α, x)-diagram, which contains all the information needed to perform the convolution at a glance. The precise definition of this method is lengthy, but its implementation is simple, since it results in an uncomplicated diagram involving only straight lines from which it is possible to determine the range of integration and the appropriate integrand.
There is an alternative method for finding the limits in the CCO defined by Zhang Zuhao in “The Square Matrix Rule of the Convolution Integral,” published in 1990 in IEEE Transactions on Education.
In addition to these two methods, there is the graphical solution method, whose origin comes from the graphical interpretation given in [2, p. 232], as cited in early in this article. Jack D. Gaskill presented a naïve description of this method in his more than fabulous book concerning linear systems, Fourier transforms, and optics [12].

Books About the CCO

The CCO has been present, in a minor or major magnitude, in any book related to the theory and applications of Fourier or Laplace transforms. A consequence of this fact is that there are only a small number of published books and theses dealing broadly with its theory and applications. The following list of books on the CCO, in which papers and lecture notes are not considered, demonstrates this.

• Books about the foundations of the CCO theory from the point of view of classical mathematical analysis: [10], [13]–[17].
• Books about the treatment of the CCO by the theory of operational calculus developed by Mikusin´ski: [18]–[23].
• Books about the application of the CCO to DEs, integral transforms, and shape of functions: [10], [24], and [25].
• Books about the application of the CCO to physics and engineering: [16], [26]–[29].
• Books about the application of the CCO to approximation of functions: [30]–[34].

 Final Words: The Hidden Story of Convolution

In the aforementioned paper by Cartier, it is pointed out that “[the CCO] can strike terror in the heart of the average engineer.” I hope this paper familiarizes users with the CCO enough to reduce the terror provoked by it, or at least prevents them from succumbing to mysticism.
To recapitulate, the CCO started its history in the 1760s, but it was not until the end of the 19th century that it received its first name. At the beginning of the 20th century, it earned a general name and notation to represent the effect of folding, translating, multiplying, and integrating.
Since Euler conceived it in its more general form, its theory has been linked to the theory of DEs and, in the 19th and 20th centuries, to the theory of integral equations. Moreover, together with the use and development of the CCO, another development was the theory of integral transforms, a theory that has also been proved very useful in applied mathematics and engineering. The theories were born almost at the same time and may be considered twins. In fact, as Isidore Isaac Hirschman (1992–1990) and David Vernon Widder (1898–1990) established in their book, the CCO can be, after some variable substitutions, converted to integral transform formulae [10].
As is sometimes the case in the development of twins, one of them is dominant with respect to the other one. This is the case: the dominant child has been the theory of integral transforms since the theory of the CCO has been overshadowed by it. This fact can clearly observed by two main occurrences:

• The theory of a particular CCO is generally described as part of the theory of an integral transform.
• The number of books concerning the theory of the CCO is small compared to the number of books concerning integral transforms.

Despite these facts, the CCO has its own history, and now it is time to be let it be known to the applied mathematics and engineering community. The description of its history has just begun.

References

1. G. Doetsch, Theorie und Anwendung der Laplace-Transformation. New York: Dover, 1943.
2. M. F. Gardner and J. L. Barnes, Transients in Linear Systems: Lumped-Constant Systems, 16th ed., vol. I. New York: Wiley, 1963.
3. N. Bourbaki, Eléments d’Histoire des Mathématiques, 2ed. Paris, France: Hermann Editeurs des Sciences et des Arts, 1969.
4. J. A. Domínguez-Torres. (2014, Apr. 19). The origin and history of convolution I: continuous and discrete convolution operations. [­Online]. Available: http://www.slideshare.net/Alexdfar/origin-adn-history-of-­convolution
5. J. Miller. (2011, Mar. 13). Earliest known uses of some of the words of mathematics. [Online]. Available: http://jeff560.tripod.com/mathword.html
6. L. Euleri, Institutionum Calculi Integralis, vol. 2. Petropoli: Impensis Academiae Imperialis Scientiarum, 1768.
7. L. Evlero, “Constrvctio aeqvationis differntio-differentialis Aydu+(B+Eu+Fuu)ddy)=0 fumto elemento du conftante,” Novi Commentarii Academiae Scientiarum Petropolitanae, vol. 8, pp. 150–156, 1763.
8. H. K. Burkhardt, Jahresbericht der Deutschen Mathematiker-Vereinigung (Vols. Zehnter Band, Zweites Heft). Leipzig, Deutschland: Teubner, 1908.
9. J. B. Fourier, Théorie Analytique de la Chaleur. Oeuvres de Fourier, vol. I. Paris, France: Gauthier-Villards et Fills, 1888.
10. I. I. Hirschman and D. V. Widder, The Convolution Transform. New York: Dover, 2005.
11. E. B. Hall and G. L. Wise, “An algebraic aspect of linear system theory,” IEEE Trans. Circuit Syst., vol. 37, no. 5, pp. 651–653, 1990.
12. J. D. Gaskill, Linear Systems, Fourier Transforms and Optics. New York, USA: Wiley, 1978.
13. H. Bergström, Limit Theorems for Convolutions. Stockholm, Sweden: Almqvist & Wiksell, 1963.
14. I. H. Dimovski, Convolutional Calculus, 2nd ed. Dordrecht, The Netherlands: Kluwer, 1990.
15. W. Kecs, The Convolution Product and Some Applications. Bucharest, Romania: Editura Academiei and D. Reidel, 1982.
16. R. Maurice, Convolution and Fourier Transforms for Communications Engineers. London, U.K.: Pentech Press, 1976.
17. H. M. Srivastava and R. G. Buschman, Theory and Applications of Convolution Integral Equations. Dordrecht, The Netherlands: Springer Science+Business Media, 1992.
18. L. Berg, Operatorenrechnung. Band I: Algebraische Methoden. Berlin, ­Deutschland: VEB Deutscher Verlag der Wissenschaften, 1972.
19. L. Berg, Operatorenrechnung. Band II: Funktionentheoretische Methoden. Berlin, Deutschland: VEB Deutscher Verlag der Wissenschaften, 1974.
20. I. H. Dimovski, Convolutional Calculus, 2nd ed. Dordrecht, The Netherlands: Kluwer, 1990.
21. V. Ditkine and A. Proudnikov, Calcul Opérationel. Moscou, Sovetskij Soyuz: Mir, 1979.
22. H.-J. Glaeske, A. P. Prudnikov, and K. A. Skòrnik, Operational Calculus and Related Topics. Boca Raton, FL: Chapman & Hall, 2006.
23. J. G. Mikusin´ski, Rachunek Operatorów. Warsaw, Poland: Polskie Towarzystwo Matematyczne, 1953.
24. J. A. Domínguez-Torres, “Fourier-based methods in CAD,” Ph.D. dissertation, Cranfield Institute of Technology, Applied Mathematics and Computing Group. Cranfield, U.K.: Cranfield Institute of Technology, 1992.
25. W. Kecs, The Convolution Product and Some Applications. Bucharest, Romania: Editura Academiei and D. Reidel Publishing Company, 1982.
26. A. Girard, L’Inversion du Produit de Convolution en Physique (mise au point bibliographique). Chatillon: Office National d’Études et de Recherches Aérospatiales, 1967.
27. P. A. Jansson, Ed. Deconvolution of Images and Spectra, 2nd ed. New York: Dover, 2012.
28. R. C. Jenninson, Fourier Transforms and Convolution for the Experimentalist. Oxford, U.K.: Pergamon Press, 1961.
29. M. Tournarie, “L’inversion du produit de convolution en physique,” Comptes Rendus Hebdomadaires des Séances de l’Académie des Sciences, vol. CCXLI, pp. 1923–1925, 1955.
30. P. L. Butzer and R. J. Nessel, Fourier Analysis and Approximation, vol. 1. New York: Academic, 1971.
31. U. Dini, Serie di Fourier e altre Rappresentazioni Analitiche delle Funzioni di una Variable Reale. Pisa, Italia: Tipografia T. Nistri e C, 1880.
32. E. W. Hobson, The Theory of Functions of a Real Variable and the Theory of Fourier’s Series, 2nd ed., vol. II. Cambridge, U.K.: Cambridge Univ. Press, 1926.
33. H. S. Shapiro, Smoothing and Approximation of Functions. New York: Van Nostrand Reinhold, 1969.
34. R. M. Trigub and E. S. Belinsky, Fourier Analysis and Approximation of Functions. Dordrecht, The Netherlands: Kluwer, 2004.