Mathematical modeling of physiological systems is a fundamental milestone of biomedical engineering. Models allow for the quantitative understanding of the intimate functions of a biological system, estimating parameters that are not accessible to direct measurement and performing in silico trials by simulating and tracking a physiological system in case its function has been deranged. Modeling has always been central in the Italian biomedical engineering community. Here, we review the progress in two areas: glucose and neurocomputational modeling with an emphasis on their clinical impact.
Glucose Modeling
The glucose system has received considerable interest in recent decades due to the growing prevalence of diabetes [1].
Models to Measure: Minimal
Minimal (coarse-grained) models—as opposed to maximal (fine-grained) models discussed later—are parsimonious descriptions of the key components of the system and are capable of measuring the crucial processes of glucose metabolism [2].
Glucose and Insulin Fixes
Glucose
Glucose production and utilization vary as an effect of a perturbation, e.g., a meal, due to endocrine and nervous control mechanisms. Glucose tracers and models are needed to estimate the rate of appearance, Ra, and disappearance, Rd, of glucose. New experimental guidelines for the accurate estimation of Ra and Rd have been developed, particularly the tracer-to-tracee clamp technique with stable isotopes. Depending on the question being asked, both dual and triple tracer protocols can be used.
Insulin
To quantitatively assess an insulin secretion profile after a glucose stimulus, a deconvolution method is needed. However, it is not possible to reconstruct pancreatic secretion from plasma insulin concentration since insulin is secreted in the portal vein and then degraded by the liver before appearing in circulation. This problem was bypassed by using C-peptide—secreted equimolarly with insulin, but not extracted by the liver—and the state-of-the-art method is the stochastic deconvolution.
Insulin and Glucose Control
Insulin
To assess insulin control, an intravenous glucose tolerance test (IVGTT), an oral glucose tolerance test (OGTT), or a mixed-meal glucose tolerance test (MTT) must be used. Linear dynamic models are too simplistic to describe insulin action. The concept of minimal parsimonious models was introduced and allowed us to arrive at a nonlinear model with glucose kinetics described with one compartment and remote (with respect to plasma) insulin controlling both the net hepatic glucose balance and the peripheral glucose disposal. The model provides an index of insulin sensitivity, which was validated in numerous studies and employed in more than 1,000 papers. This index does not account for how fast or slow insulin action takes place: A new dynamic index was later introduced to also account for the timing of insulin action in addition to the magnitude. Glucose kinetics requires at least a two-compartment model: Undermodeling the system underestimates insulin sensitivity. An improved two-compartment glucose minimal model has been proposed in a Bayesian maximum a posteriori (MAP) context.
IVGTT establishes glucose and insulin concentrations that are not seen in normal life. It is desirable to measure insulin sensitivity in the presence of physiological conditions, e.g., during MTT or OGTT. For this purpose, the oral glucose minimal model has been developed [Figure 1(a)] by using a parametric function describing the rate of glucose appearance in plasma through the gastrointestinal tract. This added complexity renders the model nonidentifiable, i.e., there is the need to assume some parameter values and to use a MAP estimator. The model provides an index of insulin sensitivity, which has also been validated. Also for MTT/OGTT, a dynamic insulin sensitivity index can be calculated.
![FIGURE 1 - The (a) glucose and (b) C-peptide oral minimal models. (c), (d) A schematic diagram to illustrate the importance of expressing beta-cell responsivity in relation to insulin sensitivity by using the disposition index (DI) metric [i.e., the product of beta-cell responsivity times insulin sensitivity (SI) is assumed to be a constant]. (c) A normal subject (state I) reacts to impaired SI by increasing beta-cell responsivity (state II), while a subject with impaired tolerance does not (state 2). In state II, beta-cell responsivity is increased but the disposition index (DI) is unchanged, and normal glucose tolerance is retained normal, while in state 2, beta-cell responsivity is normal but not adequate to compensate for the decreased SI (state 2), and glucose intolerance is developed. (d) Impaired glucose tolerance can arise due to defects of beta-cell responsivity and/or defects of SI. In this hypothetical example, subject x is intolerant due to his poor beta-cell function, while subject y has poor SI. The ability to dissect the underlying physiological defects (SI or beta-cell responsivity) allows us to optimize medical treatments, i.e., these two individuals need opposite therapy vectors.](https://www.embs.org/wp-content/uploads/2015/07/fig17.jpg)
Both the IVGTT and MTT/OGTT minimal models provide a net effect measure of insulin action, i.e., the ability of insulin to inhibit glucose production and stimulate glucose utilization. It is possible to dissect insulin action into its two individual components by adding a glucose tracer to the IVGTT or MTT/OGTT. The labeled IVGTT single-compartment model came first and was later improved by a two-compartment version. More recently, a stable, labeled MTT/OGTT model was developed that provides validated indices of disposal and liver insulin sensitivity.
While whole-body models can provide an overall measure of insulin action, it is important to measure insulin action at the organ/tissue level, e.g., the skeletal muscle, by quantitating the effect of insulin on the individual steps of glucose metabolism, i.e., transport from plasma to interstitium, transport from interstitium to cell, and phosphorylation. Understanding which metabolic step is impaired can also guide a targeted therapeutic strategy. Direct measurement of these individual steps is not possible, and the most recent model-based approach is based on positron emission tomography (PET). A five-rate-constant model is needed for studying glucose metabolism in the skeletal muscle from [18F]fluorodeoxyglucose ([18F]FDG) data. The model has revealed inefficient transport and phosphorylation [18F]FDG rate constants in obesity and type 2 diabetes as well as the plasticity of the system; i.e., defects can be substantially reversed with weight loss. From [18F]FDG modeling, only glucose fractional uptake, not glucose transport and phosphorylation rate constants, can be estimated. To this end, a multiple-tracer approach has been proposed with three different PET tracers injected sequentially.
Insulin
A mechanistic description of pancreatic insulin secretion is needed to quantitate indices of beta-cell function. This was first proposed for first- and second-phase IVGTT and later for MTT/OGTT. Two responsivity indices were derived related to the dynamic (i.e., proportional to the rate of change) and the static (i.e., proportional to) glucose control. Since the glucose–insulin system is negative feedback, beta-cell function needs to be interpreted in light of the prevailing insulin sensitivity. One possibility is to resort to a normalization of beta-cell function based on the disposition index (DI) paradigm. This concept is clearly illustrated above in Figure 1(c) and (d): Beta-cells’ ability to respond to a decrease in insulin sensitivity needs to be counteracted by an increase of insulin secretion. The disposition paradigm allows for not only assessing whether the two phases of beta-cell function are appropriate in light of the prevailing insulin sensitivity but also monitoring their variations in time and quantifying the effect of different treatment strategies.
Models to Simulate: Maximal
Large-scale maximal (fine-grain) models are needed for simulation. These models are comprehensive descriptions that attempt to fully implement the body of knowledge about a system into a generally large, nonlinear model of high order with several parameters [3].
Theories of Insulin Secretion
The dynamics of insulin secretion was investigated in the 1960s and 1970s in the perfused pancreas mainly from the rat. A model-based theory was proposed where insulin was located in packets. Recently, an update of the model has been put forward based on data of cell-to-cell heterogeneity with respect to their activation threshold. By using multiscale modeling, the relation between the subcellular events described in this model and the beta-cell minimal model indices has been also investigated.
In Silico Experiments in Type 1 Diabetes
There are situations in which in silico experiments with large-scale models could be of enormous value. In fact, it is often not possible, appropriate, convenient, or desirable to perform an experiment on a system because it cannot be done at all or is too difficult, too dangerous, or unethical. In such cases, simulation offers an alternative form of in silico experimentation on the system. A number of simulation models have been published in the last four decades, but their impact has been very modest in the control of type 1 diabetes. In fact, all these models were “average,” meaning that they are only able to simulate the average population dynamics, not the interindividual variability. The average-model approach is not sufficient for realistic in silico experimentation with control scenarios, where facing with intersubject variability is particularly challenging.
Building on the large-scale model developed in the healthy state from a rich triple tracer meal data set, a type 1 diabetes simulator has been developed that can realistically describe intersubject variability. This was a paradigm change in the field of type 1 diabetes: For the first time, a computer model has been accepted by the U.S. Food and Drug Administration as a substitute of animal trials for certain insulin treatments. In this simulator, a virtual “human” is described as a combination of several glucose, insulin, and glucagon subsystems (Figure 2).
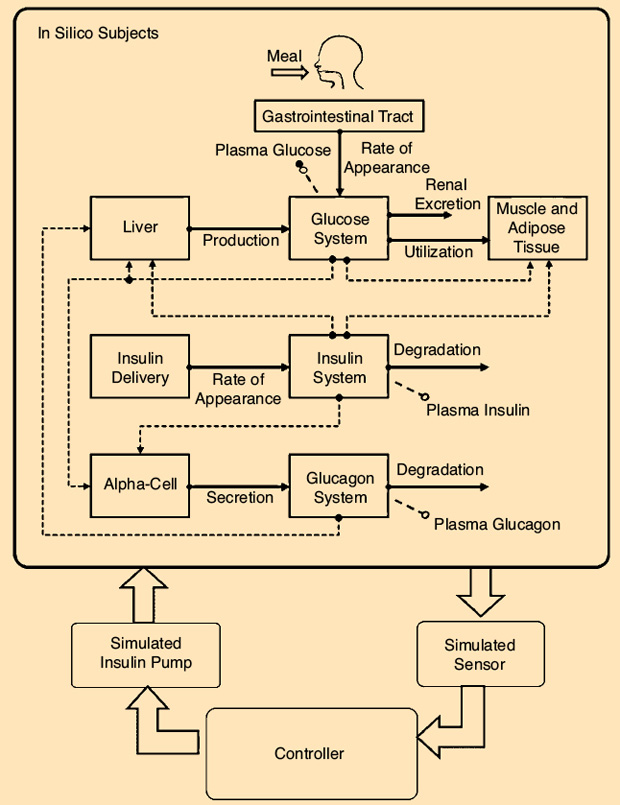
In summary, the model consists of 13 differential equations and 35 parameters for each subject. The simulator is equipped with 100 virtual adults, 100 adolescents, and 100 children, spanning the variability of the type 1 diabetes population observed in vivo. Each virtual subject is represented by a model parameter vector, which is randomly extracted from an appropriate joint parameter distribution. This simulator has been adopted by the Juvenile Diabetes Research Foundation (JDRF) Artificial Pancreas Consortium and has allowed an important acceleration of closed-loop studies with a number of regulatory approvals obtained based on simulation only. The simulator has been used by 32 research groups in academia and by five companies active in the field of diabetes and has led to 63 publications in peer-reviewed journals.
Models to Control
A patient with type 1 diabetes faces a lifelong behavior-controlled optimization problem: The administration of external insulin to control glycemia enters a stochastic scenario where hyperglycemia and hypoglycemia may not be easily prevented by standard open-loop therapy. To restore the missing loop, a system combining a glucose sensor, a control algorithm, and an insulin infusion device is needed: the so-called artificial pancreas (AP). Recently, thanks to technological progress in both subcutaneous (SC) glucose sensing and insulin delivery, the development of new controllers known as model-predictive control (MPC) and the possibility of performing in silico trials have resulted in an increase in AP research, which is also facilitated by support from several bodies, including the JDRF, the National Institutes of Health, and the European Union.
The new wave of SC AP based on MPC uses prediction of glucose dynamics by using a model of the patient and, as a result, appears better suited for mitigation of time delays due to SC glucose sensing and insulin infusion. MPC also allows us to incorporate constraints on the insulin delivery rate and glucose values that safeguard against insulin overdose or extreme BG fluctuations and can cope with inter- and intrapatient variability. Another important design element is the concept of the modular approach to AP design, which has the advantage of allowing sequential development, clinical testing, and ambulatory acceptance of elements (modules) of the closed-loop system. The various modules have different responsibilities, such as the prevention of hypoglycemia, postprandial insulin correction boluses, basal rate control, and administration of premeal boluses, and act on different time scales. This modular MPC algorithm has been successfully employed in two hospital trials, showing reduced average glucose without increasing patients’ risk for hypoglycemia.
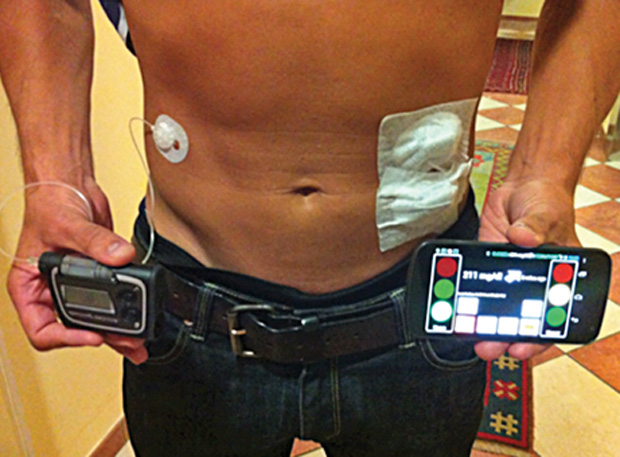
However, none of these previous systems had an AP system suitable for outpatient use. The critical missing features were portability and a user interface designed to be operated by the patient. The AP transition to portability and ambulatory use began in 2011 with the introduction of the Diabetes Assistant (DiAs)—the first portable outpatient AP platform, which uses an Android smartphone as a computational platform (Figure 3). In October 2011, the wearable DiAs-based AP was used in two outpatient pilot trials done simultaneously at the universities of Padova, Italy, and Montpellier, France. These two-day trials enabled a series of feasibility and efficacy studies of ambulatory closed-loop control conducted at the universities of Virginia, Padova, and Montpellier, and at Sansum Diabetes Research Institute, Santa Barbara, California. Recently, an outpatient multinight bedside closed-loop control study has been completed, showing a significant improvement in morning and overnight glucose levels and time in the target range. At present, multisite randomized crossover trials of two months are being conducted in an outpatient setting.
Neurocomputational Modeling
The study of neural mechanisms with mathematical models (a subject often named “computational neuroscience”) is a relatively new discipline that is becoming crucially important within the field of neuroscience. It aims at providing a better understanding of brain function and converting this knowledge into neurological clinical applications. For the sake of simplicity, in the following sections, three main problems will be considered within the domain of computational neuroscience, although this distinction is often more didactical than real.
Connectivity
A classical problem in modern neuroscience consists in finding the connectivity patterns among brain regions during specific cognitive tasks. The basic idea is that the brain can be described as a network, i.e., a connected system of units (representing specialized regions in the brain) linked via communication pathways. In fact, even the solution of simple cognitive problems requires the participation of many different specialized regions that are recruited during the task and reciprocally exchange information in a temporally dependent way so that the activity in one region is influenced by the temporal activity in the others. The use of connectivity graphs is fundamental to summarize this information-exchange process and to follow its alterations in neurological disorders.
Astolfi et al. used time-varying multivariate autoregressive models to describe the interactions among cortical areas based on Granger causality, starting from high-resolution electroencephalography (EEG) recordings [4]. They demonstrated that this approach allows for the estimation of rapidly changing influences between the cortical areas during simple motor tasks. An important aspect of most connectivity studies is that the cortical activities in the regions of interest (from which the autoregressive models are estimated) are reconstructed from scalp EEG using a realistic geometry head volume conduction model. Data obtained with the previous models are generally summarized using the graph theory for which a large body of indexes and tools are available in the literature: The final network is represented by means of an oriented graph from which the main connectivity parameters can be assessed in objective quantitative terms. These techniques may have important clinical applications since connectivity patterns are altered in neurological pathologies such as schizophrenia, brain reorganization after a stroke, or following motor imagery-based brain–computer interface training.
EEG and fMRI Fusion
A second important modeling problem in computational neuroscience concerns the relationship between EEG and functional magnetic resonance imaging (fMRI). The two techniques, in fact, are mutually complementary: EEG exhibits a good temporal resolution but poor spatial precision; conversely, fMRI exhibits very good spatial resolution but poor temporal discrimination capacity. Furthermore, the two techniques measure different quantities (i.e., EEG measures electrical activity and fMRI measures metabolism changes). The best way to fuse data from the two techniques is to build mathematical models that are able to integrate both aspects in a coherent framework. In this regard, some authors used autoregressive models estimated from cortical sources derived from EEG data: Determination of the priors in the resolution of the linear inverse problem can be performed with the use of information from the hemodynamic responses, as revealed in the cortical areas by fMRI. Another approach makes use of neural mass models; in these, individual components of the network consist of oscillatory circuits that are able to simulate EEG waves and relate them with metabolic neuron activity. A possible clinical application of these models concerns not only the interpretation of EEG patterns and their relation with fMRI but also the study of brain waves, such as those occurring during epilepsy, sleep, or high cognitive tasks.
Biologically Inspired Neural Networks
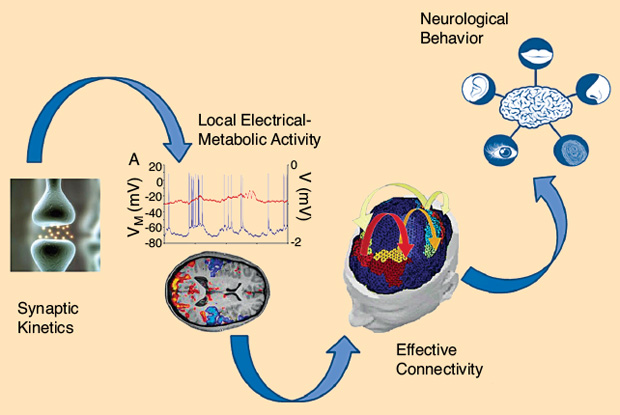
Finally, an important research field concerns the construction of biologically inspired neural networks. Their aim is to gain a deeper understanding of the neurophysiological mechanisms underlying some cognitive processes, such as memory, perception, and attention. In these models, as shown in Figure 4, the activity of individual neural groups is described using equations inspired by the physiology (either using spiking neurons or rate neurons, i.e., neurons whose output is proportional to the firing rate) connected via reliable synapses; emphasis is given to the topology of the network and to the synaptic relationships (excitatory or inhibitory) among neurons.
The results can be used to not only simulate physiological data but also mimic behavioral experiments. These models differ from those summarized previously in two main aspects. First, the individual neurons and their connections must have a clear neurophysiological counterpart (although largely simplified); i.e., the topology is established a priori on the basis of neurophysiological knowledge rather than being derived a posteriori from data. Second, synapses are plastic and can be trained using physiological learning rules to simulate the emergence of cognitive behavior from experience. Several authors have employed these models to simulate different cognitive processes. Some used a neural network model to simulate semantic memory and its relationship with language or to study the foundation of human mathematical learning [5].
The clinical benefits of these models lie in the possibility to understand the origin of neurological semantic disorders in which patients show the inability to recognize objects belonging to individual categories. Another crucial problem on which many modeling efforts are presently devoted concerns multisensory integration, i.e., the ability of the brain to link information from different sensory modalities (i.e., visual, auditory, or tactile) to improve the perception of external events in difficult or noisy conditions [6]. In neurology, multisensory models can be exploited to design or optimize clinical procedures for the rehabilitation of neurological patients with individual sensory deficits. (For instance, patients with visual deficits can be helped by the use of congruent multisensory audiovisual stimuli.)
A part of the brain that has been extensively investigated with mathematical models is the hippocampus, a bilateral subcortical temporal region implicated in individual episodic memory and in allocentric spatial navigation. A peculiarity of hippocampal circuits consists in the strong feedback connections among neurons, which self-organize during storage, resulting in a typical attractor dynamics. The dynamics of these models is further complicated by the presence of oscillating patterns (such as theta waves in the range of 4–7 Hz), which flexibly coordinate the hippocampal regions. Models explain how such waves support a flexible associative memory formation and retrieval and allow for the memorization of a list of items, such as during the recovery of a whole trajectory in a spatial navigation task. In clinics, these models may help understanding important neurological deficits such as schizophrenia and, above all, Alzheimer’s disease, in which the hippocampus is one of the first regions to be damaged, resulting in memory loss and disorientation.
Lastly, the basal ganglia, a brain structure implicated in action selection and in the initiation and termination of movements, has received much modeling attention in the past due to its crucial role in Parkinson’s disease. In particular, dopamine depletion in the basal ganglia of Parkinson’s patients gives rise to both motor and postural as well as learning impairments. Cellular-based models of the basal ganglia allow the analysis of the role of deep brain stimulation for the treatment of these patients. The results are comparable with clinical and experimental evidence on the effect of deep brain stimulation.
In summary, it is ever more apparent that mathematical modeling is having an influence on clinical practice in situations where direct measurement would otherwise be impossible. In the future, it is likely that our understanding of physiological systems will continue to improve as modeling systems become more sophisticated, leading to a commensurate advance in treatment options for patients with diabetes or neurological deficits.
References
- C. Cobelli, C. Dalla Man, G. Sparacino, L. Magni, G. De Nicolao, and B. P. Kovatchev, “Diabetes: Models, signals, and control,” IEEE Rev. Biomed. Eng., vol. 2, pp. 54–96, Jan. 2009.
- C. Cobelli, C. Dalla Man, M. G. Pedersen, A. Bertoldo, and G. Toffolo, “Advancing our understanding of the glucose system via modeling: A perspective,” IEEE Trans Biomed. Eng., vol. 61, pp. 1577–1592, May 2014.
- C. Cobelli, E. Renard, and B. Kovatchev, “Artificial pancreas: Past, present, future,” Diabetes, vol. 60, pp. 2672–2682, Nov. 2011.
- L. Astolfi, F. Cincotti, D. Mattia, M. G. Marciani, L. A. Baccala, F. de Vico Fallani, S. Salinari, M. Ursino, M. Zavaglia, L. Ding, J. C. Edgar, G. A. Miller, B. He, and F. Babiloni, “Comparison of different cortical connectivity estimators for high-resolution EEG recordings,” Hum Brain Mapp., vol. 28, no. 2, pp. 143–157, 2007.
- M. Ursino, C. Cuppini, and E. Magosso, “A neural network for learning the meaning of objects and words from a featural representation,” Neural Netw., vol. 63, pp. 234–253, Mar. 2015.
- C. Cuppini, E. Magosso, N. Bolognini, G. Vallar, and M. Ursino, “A neurocomputational analysis of the sound-induced flash illusion,” Neuroimage, vol. 92, pp. 248–266, May 2014.