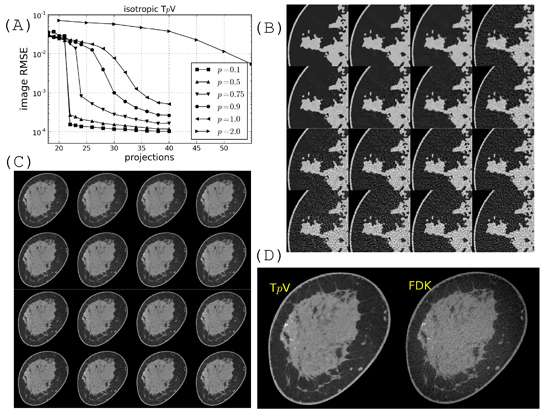
Exploiting sparsity in the image gradient magnitude has proved to be an effective means for reducing the sampling rate in the projection view angle in computed tomography (CT). Most of the image reconstruction algorithms developed for this purpose solve a nonsmooth convex optimization problem involving the image total variation (TV). The TV seminorm is the `1 norm of the image gradient magnitude, and reducing the `1 norm is known to encourage sparsity in its argument. Recently, there has been interest in employing nonconvex `p quasinorms with 0 < p < 1 for sparsity exploiting image reconstruction, which is potentially more effective than `1 because nonconvex `p is closer to `0 – a direct measure of sparsity. This work develops algorithms for constrained minimization of the total p- variation (TpV), `p of the image gradient. Use of the algorithms is illustrated in the context of breast CT – an imaging modality which is still in the research phase and for which constraints on X-ray dose are extremely tight. The TpV-based image reconstruction algorithms are demonstrated on computer simulated data for exploiting gradient magnitude sparsity to reduce the projection view angle sampling. The proposed algorithms are applied to projection data from a realistic breast CT simulation, where the total X-ray dose is equivalent to two-view digital mammography. Following the simulation survey, the algorithms are then demonstrated on a clinical breast CT data set.
View full article